数学で重要な小学校算数の基礎スキルとは
中学校数学で重要な小学校算数の基礎スキルを整理するには
まず、算数と数学の違いを知ることが必要です。
算数と数学の違いとは
NHK番組「チコちゃんに叱られる!」2020.9.18放送内容をもとにすると次のようになります。
・数学を学ぶ目的は「問題を整理して答えを導くことで論理的な思考を身につける」というもの。
中学1年生は論理的な思考を身につける入り口付近にいることになります。
その中学1年数学の壁をクリアするために重要となる算数の基礎スキルは2つです。
② 単位量あたりの大きさの「単位換算が説明しながらできる」こと(b)
問題を整理して答えを導くことに必要だからです。

途中の式と答えの「途中の式」を大事にするという考え方(a)
中学の数学で大事なのは「どう計算したか」という答えの導き方です。
答えの導き方、すなわち、問題を整理して答えを導いた道筋がわかる「途中の式」です。
しかし、数学が苦手な生徒の認識は
どう計算した すなわち、「途中の式」ではなく、答えが出せればいいと認識です。
具体例をあげると
答 6 cm
どう計算した?
と聞くと
2+2+2 または 2×3 と答える
数学が苦手な生徒は
「暗算で計算した」または、質問の意味が分からず答えられない
なぜ途中の式が必要かといえば、
一辺が a cmの正三角形の周りの長さは?
という問題ならば、
途中の式が書ければ、
a+a+a a×3
答 3a cm
と 2 を a に置き換えるだけで、答えが出せるからです。
中学校で大事なのは「どう計算した?」という答えの導き方、すなわち「途中の式」です。
数学が苦手な生徒は
「途中の式」ではなく、6cm といった答えが重要と認識しています。

単位量あたりの大きさの「単位換算」が説明しながらできること(b)
問題を整理して答えを導くことに一番有効でまた重要なのは時速の単位換算です。
という定義の理解をもとに
分速〇mへの単位変換が
途中の考え方を説明しながらできる
単位量あたりの大きさに関する題材として、
「時速」に関しては
中学校でも確実に例題として出てきます。
その次に多く出るのが「単位時間当たりの水の量」だからです。
時速を秒速に単位換算するのは難しいですが、時速→分速→秒速と単位換算練習が望まれます。
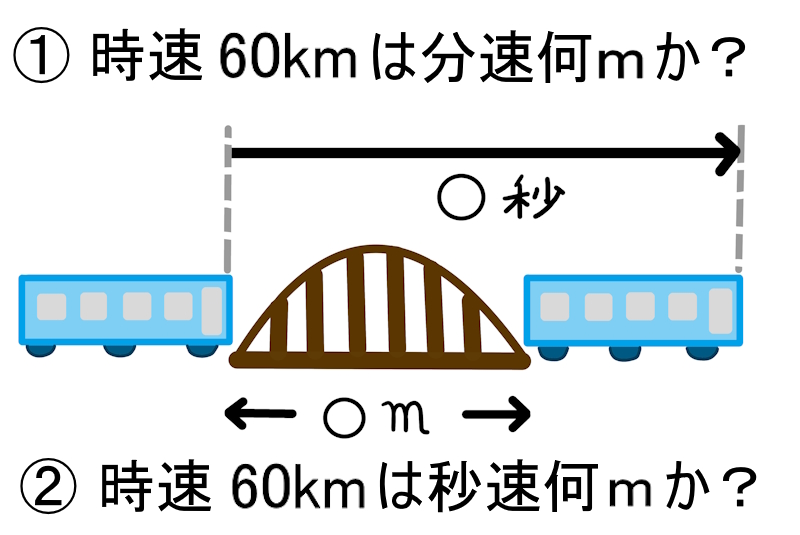
道のり、速さ、時間の
計算関係を表したみはじ図を覚えるよりも、
時速・・・1時間に進む道のり
[例] 時速5km・・・1時間に5km進む速さ
と定義を覚え、
単位換算をすることが、
確実な理解につながります。
なお、
比べられる量、もとにする量、割合の
計算関係を表した
くもわ図を覚えている児童もありますが、
あとで解説しますが、
中学校では比例式を作り、方程式を解くという考え方で
問題を整理して解きますから、
中学校では
くもわ図を使うことは、ほぼありません。
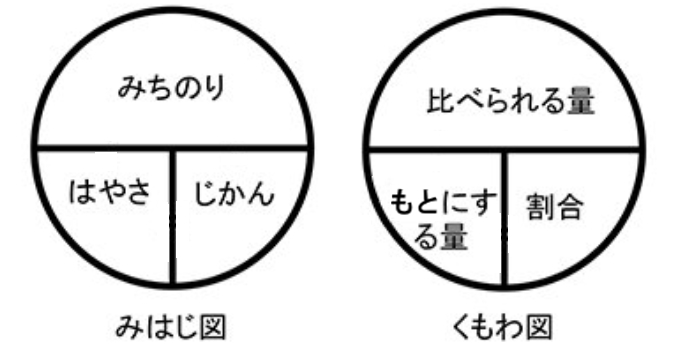
割合に関するくもわ図を知っている生徒もいます。
基礎スキルと応用問題の違いは論理的な思考のあるなし
小学校の応用問題は、
その応用問題を解くための途中の考え方が論理的思考の基盤となるもの
です。
小学校では、
「割合」に関わる問題を解く過程で、
パターン化を図ることで基盤つくりをすることが多いです。
基盤つくりで注意すべきことや必要になることは次の3つです。
② 分数の割り算は、なぜ逆数をかけるか?
③ 論理的な思考とは(a)(b)を組み合わせて解くスキルのこと
「割合」の問題を整理して答えを導くにあたり、
分数の割り算は必須のものだからです。
また、単位量あたりの大きさの単位換算の考え方と「割合」は共通点が多いからです。
しかし、「割合」の問題の解き方は小学校と中学校で異なるので、
注意が必要です。
考え方(思考)が小学中学で異なり、中学でほぼ使わなくなる応用問題もある
「割合」の応用問題について
小学校では
割合の3用法として、答えの導き方を整理します。
中学校では、
比例式、方程式を用いて解くようになります。
詳しくは見出し
論理的な思考とは(a)(b)を組み合わせて解くスキルのこと
で、具体的に問題を紹介しながら、
異なる点を解説していきます。
小学6年生の算数では、割合については以下の 2. ~ 6. の単元で学習します。
2. 文字と式
3. 分数と整数のかけ算・わり算
4. 分数のかけ算
5. 分数のわり算
6. 比
7. 拡大図と縮図
8. 円の面積
9. 角柱と円柱の体積
10. 比例と反比例
11. 並べ方と組み合わせ方
12. データの調べ方
この「割合」に関わる応用問題は、
論理的思考の基盤となるものですが、
中学校では
問題を解くとき、
小学校の考え方を使わずに、
比例式を作り、方程式の考え方で
解きます。
そして、一度例題のようにして解くと
「速さ」「単位時間に出る水の量」というタイプの問題以外は
その後、教科書に出てくることは、ほぼありません。

分数の割り算は、なぜ逆数をかけるか?
等分除と包含除がわかって入れば、理解がしやすい。
30個の飴を一人5個ずつ分けた。何人に分けられか?(包含除)
等分除
何等分かに分けるということです。
包含除
上記であれば、30個の中に5個がいくつ含まれるか
ということです。
という割り算ならば、
例えば、
5個のチョコレート(キットカット)の中には、
1/2個のチョコレート(キットカット)が
いくつ含まれるか?
ということになります。

チョコレート(キットカット)は10人に分けられる
かまぼこ3本の中に
3/5はいくつあるか

左のかまぼこを15ヶに分けて考えます。
こう考えると、
3÷ 3/5 = 3 × 5/3 と 割り算は、逆数をかけることが理解できます。
しかし、実は、
論理的な思考の基盤として、割り算はなぜ逆数をかけるか
は、あまり重要ではありません。
中学校では、
生徒から「なぜ?」という質問が出た時に、
興味関心を高める一つの手立てとして、
説明をしています。
アウトプット勉強法というのがあります。
人に説明をすることで理解を確かなものにする方法です。
なぜ、分数の割り算は逆数をかけるのかを知り、
家で、
お父さんやお母さんや家族に話をすることで、
問題を整理して答えを導く力を伸ばす一助になれば
というあつかいをしている項目です。
論理的な思考とは(a)(b)を組み合わせて解くスキルのこと
小学6年生算数で、
応用問題、特に割合に関わる問題を解く過程で、
問題をパターン化(一般化)して解きます。
その時のポイントと注意したいことです。
② パターン化(一般化)で教師が見落としやすい生徒の理解度
パターン化(一般化)することで、
問題が解きやすくなると、
児童にとって算数学習が面白くなることにつながるからです。

パターン化(一般化)するためのポイント
割合の応用問題は、
問題文をパターン化(一般化)して、
問題を解くことを学ぶための
問題と言い換えることができます。
パターン化の手法は
割合の3用法と呼ばれます。
詳しくは以下の通りです。
ただ、中学校では、
比例式、方程式を用いて解くようになるので、
そのこともあわせて書いています。
【第1用法】割合を求める
(A)が(B)の何倍にあたるかを求める。
BをもとにしたときのAの大きさの割合pを求める方法(考え方)
3mは6/5m(1.25m)の何倍ですか?
p=A÷B
中学では B や A に分数小数が含まれる時、
方程式 A = B × □ を作り、
等式変形し、□= A ÷ B
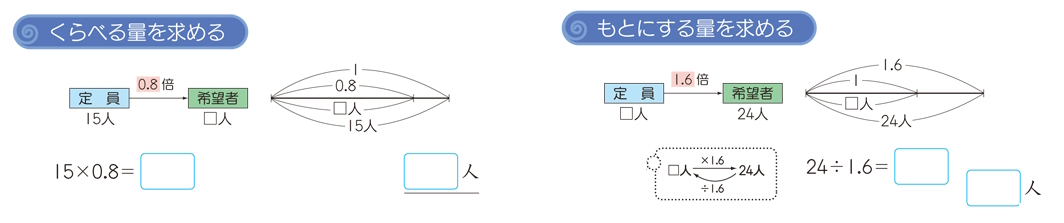
【第2用法】くらべる量を求める
〇〇中学校の募集定員は15人です。
受験者は4/5倍(0.8倍)でした。
受験者は何人ですか。
A=B×p
中学でも、受験者A=15 × 4/5
の計算をする
【第3用法】もとにする量を求める
〇〇中学校の入学受験者は24人でした。
これは募集定員の8/5倍(1.6倍)にあたります。
募集定員は何人ですか。
B=A÷p
中学では、基本扱わない。
方程式 24 ÷ □ = 8/5 を作り、
解こうとすると両辺に □ をかけることになるから。
ただし、24:□ = 8/5:1 の比例式を使うことはある。
なお、
比の値のあつかいについて、
算数と数学では、
重要度が異なる部分があります。
全体をきまった比に分ける方法(考え方)は特に重要です。
中学校において面積比の問題を解くときによく使います。
高校の図形領域では、内分点外分点の基礎知識として必要になります。
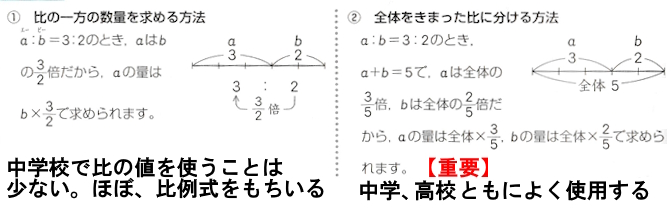
中学では、比の一方の数量を求めることはほぼないです。全体をきまった比に分ける考え方は重要です。
パターン化(一般化)で教師が見落としやすい生徒の理解度
パターン化を学ぶ上で、注意が必要なことがあります。
生徒児童によっては、
極端な例を出します。
答 120a 円
間違っているよと言うと
じゃ、
a/3 × 120 で 40a 円
答えとしては正しいですが、
この生徒は本当に理解ができているのでしょうか?
気になって、他の問題の時にもチェックしていると
答 a/7 個
といった答えを書いている時もありました。
この生徒にとっては、
2つの数をかけ算か割り算すれば答えが出る
がパターン化の理解だったのです。
何が一番の課題かというと
「わかっていない」ということが認識できない。
ということです。
見落としがちな間違いをするので、
注意が必要です。

終わりに
中学校では、
比例式、方程式の考え方を用いて解く問題が出てくる
ということを書きました。
小学校と中学校で解き方(考え方)異なるものをもう3つ、紹介しておきます。
参考になさってください。
[1] 1Lの重さが5/6kgの米が、10kgあります。この米は何Lありますか。
10÷5/6 =12
中学校
1:5/6 = □:10
比例式を作り、次に方程式を解きます
[2] 持っていたシールの3/5にあたる12枚を使いました。最初シールは何枚持っていましたか。
12÷3/5 = 20
中学校
□×3/5 = 12
方程式を作り、解きます
[3] お茶が3L入っています。9/7L飲みました。はじめにやかんに入っていた量を1としたとき、飲んだ量はどれだけにあたりますか。
9/7÷3=3/7
中学校
3:1 = 7/9:□
比例式を作り、次に方程式を解きます

